13. Volume

e1. Volume using Thin Cylinders

Finally, we consider the problem of computing the volume of a solid of revolution using thin cylinders.

The region between the functions \(y=f(x)\) and \(y=g(x)\) between \(x=a\) and \(x=b\) is rotated about the \(y\)-axis. Find the volume of the solid swept out.

For a region between a function \(y=f(x)\) and the \(x\)-axis, just set \(g(x)=0.\)

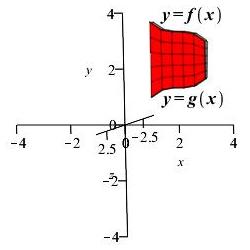
This shows the area between the functions f of x and g of x.

This is an \(x\) integral. So we chop up the \(x\)-axis, draw a vertical rectangle and rotate it obtaining a thin cylinder centered on the \(y\)-axis.

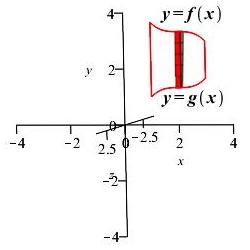
This shows a thin vertical slice of the area.

Show Hand

To approximate the volume of the cylinder, we think of the cylinder as being made from paper, cut it and unroll it into a rectangle (actually a rectangular solid). The length of the rectangle is the circumference of the circle \(L=2\pi r\). Here the radius \(r\) is equal to the position \(x\) of the cylinder within the shape. So \(L=2\pi x\). The width of the rectangle is the height of the cylinder \(W=f(x)-g(x)\). And the thickness of the rectangle is the thickness of the cylinder, namely \(\Delta x\). So the volume of the thin cylinder is approximately the volume of the rectangular solid which is: \[ \Delta V\approx LW\Delta x=2\pi x(f(x)-g(x))\Delta x \] Adding these up and taking the limit, we get the volume of the solid of revolution: \[ V=\int_a^b 2\pi x\,(f(x)-g(x))\,dx \]

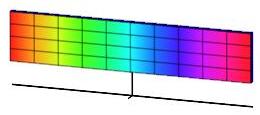
This plot shows the thin cylinder unrolled into a rectangle solid,
so that its volume may be approximated.

Now turn your head sideways A small happy face shows you to tilt your head to the right.

The region between the functions \(x=f(y)\) and \(x=g(y)\) between \(y=a\) and \(y=b\) is rotated about the \(x\)-axis. Find the volume of the solid swept out.

For a region between a function \(x=f(y)\) and the \(y\)-axis, just set \(g(y)=0.\)

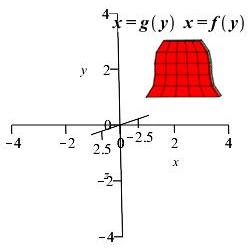
This shows the area between the functions x = f of y and g of y.

This is a \(y\) integral. So we cut up the \(y\)-axis, draw a horizontal rectangle and rotate it obtaining a thin cylinder centered on the \(x\)-axis.

The same reasoning gives the volume: \[ V=\int_a^b 2\pi y(f(y)-g(y))\,dy \]

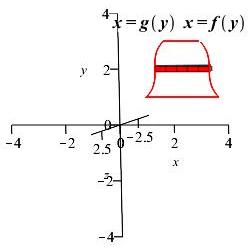
This shows a horizontal slice of the area.

Show Hand

If the region below the function \(y=f(x)\) above the function \(y=g(x)\) between \(x=a\) and \(x=b\) is rotated about the \(y\)-axis, the volume swept out is: \[ V=\int_a^b 2\pi x(f(x)-g(x))\,dx \] If the region to the left of the function \(x=f(y)\) and to the right of the function \(x=g(y)\) between \(y=a\) and \(y=b\) is rotated about the \(x\)-axis, the volume swept out is: \[ V=\int_a^b 2\pi y(f(y)-g(y))\,dy \] Both formulas can be summarized as \[ V=\int_a^b 2\pi(\text{radius})(\text{height})\,dv \] where \(dv\) is either \(dx\) or \(dy\).

Notice that finding the volume of a solid of revolution by cylinders is not a special case of finding a volume by slicing. However, the integral can still be written as \[ V=\int_a^b A(v)\,dv \] but in this case the area is the area of the cylinder, \(A=2\pi(\text{radius})(\text{height})\).

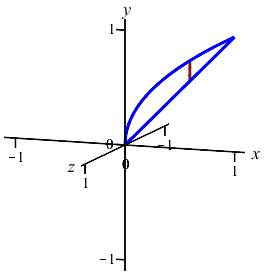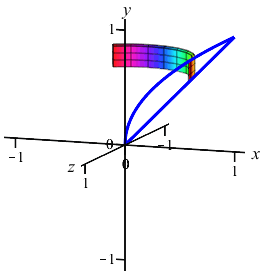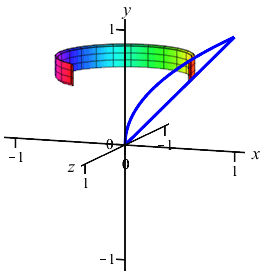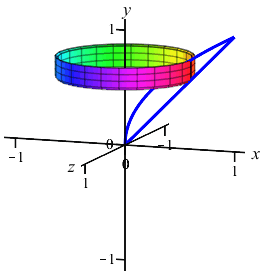
The region between the curves \(y=x\) and \(y=\sqrt{x}\) is rotated about the \(y\)-axis. Find the volume swept out. (Do the integral as an \(x\) integral.)

On the previous page, we computed this volume using washers. We now recompute it using cylinders.

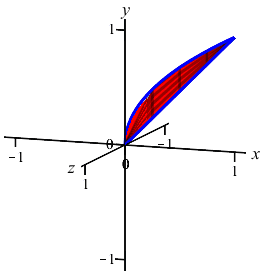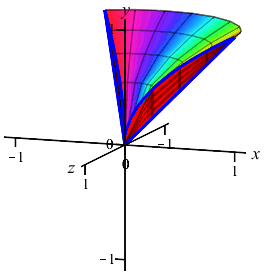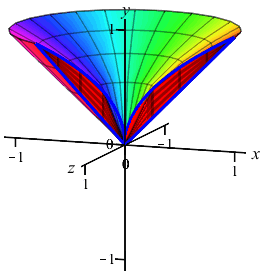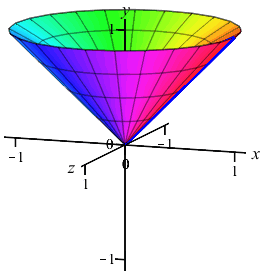
This animation shows the area between the parabola and the diagonal line
rotating about the y axis forming a solid that looks like a funnel.

Since we will be performing an \(x\)-integral, we cut up the \(x\)-axis, see that the rectangles are vertical and they rotate into thin cylinders.

So the volume is: \[\begin{aligned} V&=\int_a^b 2\pi(\text{radius})(\text{height})\,dx \\ &=\int_a^b 2\pi x(\text{upper}-\text{lower})\,dx \\ &=\int_0^1 2\pi x(\sqrt{x}-x)\,dx =\int_0^1 2\pi(x^{3/2}-x^2)\,dx \\ &=2\pi\left[\dfrac{2x^{5/2}}{5}-\dfrac{x^3}{3}\right]_0^1 =2\pi\left(\dfrac{2}{5}-\dfrac{1}{3}\right) =\dfrac{2\pi}{15} \end{aligned}\]

This animation shows a vertical slice of the area, rotating
about the y axis to form the curved surface of a cylinder.

Now you do it:

The region between the curves \(y=x\) and \(y=\sqrt{x}\) is rotated about the \(x\)-axis. Find the volume swept out. (Do the integral as a \(y\) integral.)

On the previous page, you computed this volume using washers. Now recompute it using cylinders.

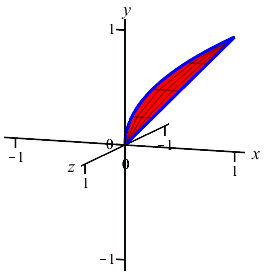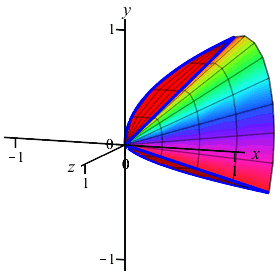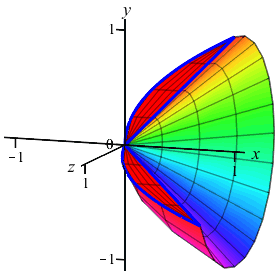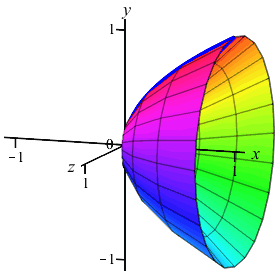
This shows the same area between the parabola opening to the right
and the diagonal line y equals x, this time rotating about the x axis.

Remember, you need to do a \(y\)-integral this time. So cut up the \(y\)-axis.

\(\displaystyle V=\dfrac{\pi}{6}\)

As functions of \(y\), the edges are at \(x=y\) and \(x=y^2\). We cut up the \(y\)-axis and see that the rectangles are horizontal rotate into thin cylinders. So the volume is: \[\begin{aligned} V&=\int_a^b 2\pi(\text{radius})(\text{height})\,dy \\ &=\int_a^b 2\pi y(\text{right}-\text{left})\,dy \\ &=\int_0^1 2\pi y(y-y^2)\,dy =\int_0^1 2\pi(y^2-y^3)\,dy \\ &=2\pi\left[\dfrac{y^3}{3}-\dfrac{y^4}{4}\right]_0^1 =2\pi\left(\dfrac{1}{3}-\dfrac{1}{4}\right) =\dfrac{\pi}{6} \end{aligned}\]

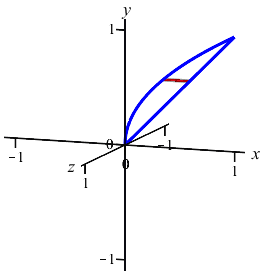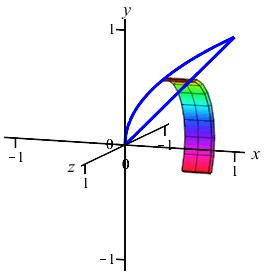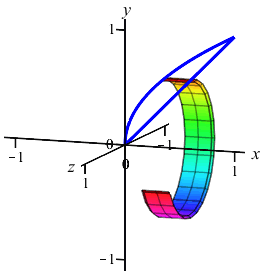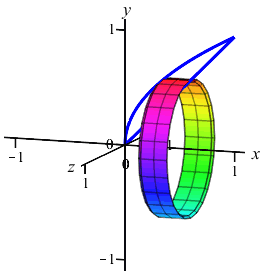
This shows a horizontal slice of the area, rotated
about the x axis to form the curved surface of a cylinder.

In the previous example and exercise, we considered volumes which could be computed using either cylinders or washers. Here is another example which can easily be computed using cylinders but would be very difficult using washers:

Example

On the next page, we will discuss the overall strategy for computing volumes of revolution.

You can practice computing Volumes of Revolution by Cylinders by using the following Maplet (requires Maple on the computer where this is executed):

Volume of a Solid of Revolution Rate It

Now, you can do all the problems: Disks, Washers and Cylinders.

13. Volume

e1. Volume using Thin Cylinders

Heading